Tanto en la numeración posicional como en la estructura discursiva cada lugar recibe su valor por su relación recíproca con los otros lugares. Por ej., el lugar de las decenas recibe su valor por estar situado entre el lugar de las unidades y el de las centenas. El lugar de la verdad en el discurso es impensable sin referirlo al lugar del goce.
El valor de un significante está determinado por su relación con los otros significantes, tanto a nivel de la diacronía como de la sincronía.
Una frase recibe su valor del contexto discursivo en el que está incluida.
El valor de una palabra depende de su relación de contigüidad, de yuxtaposición. con las otras palabras con las que comparte un lugar en la cadena sintagmática de la frase (relación de metonimia).
El valor de un fonema es consecuencia de su correlación in presentia con el conjunto de los fonemas de la palabra: f-o-n-e-m-a
Frase, palabra, fonema, reciben su valor por su relación in absentia con las otras frases, palabras, fonemas, con las que podrían formar una serie asociativa a nivel del sistema de la lengua (relación de simultaneidad).
El ser de la pera no se lo otorga su naturaleza de pera (añoranza del jardín del Edén), perdido desde siempre por mor, gracia, obra y arte, de su captura por el lenguaje.
El ser significante de la pera se lo da su con-vivencia con los otros seres de palabra con los que, de forma contingente, ex-siste: las manzanas, las ciruelas, el árbol, la deliciosa compota, el deseo del niño...
El ser significante de la pera se lo da su con-vivencia con los otros seres de palabra con los que, de forma contingente, ex-siste: las manzanas, las ciruelas, el árbol, la deliciosa compota, el deseo del niño...
 |
| La manzana matemática |
Por eso dice Lacan que el agujero es simbólico. Que se lo pregunten si no a la pera deses-perada. El título podría ser: La pera y su canción deses-perada.
 |
| La pera (el pere) agujereada |
Para saber lo que es la pera, cuál es su ser, de qué está hecha, cuál es su naturaleza, a qué sabe; en resumen, cuál es su identidad, paradójicamente, no se le puede preguntar a la propia pera, que no lo sabe, que no se puede captar a sí misma. Hay que interrogar a su Otro, a su compañera de fatigas, a su amiga del alma, a su congénere y vecina, la manzana. Absurdo lógico: para saber lo que es una pera hay que interrogar a una manzana, que, justamente, es lo que no es una pera.
El problema, y aquí está el truco, es que a la manzana le sucede lo mismo. Padece la misma dificultad, igual carencia. También ella tiene un gusano que la horada, la agujerea. Su ser, como el de la pera, sufre de una escisión. De la misma forma que la pera deberá buscar los auxilios del Otro del significante (La pera como sujeto; la manzana como Otro; ambas igualmente jodidas). La manzana no existe.
La pera piensa que la manzana puede darle la respuesta por su ser; que la manzana sabe (a esto en el psicoanálisis se le denomina técnicamente el Sujeto Supuesto Saber, que es el intríngulis de la transferencia). Pero la manzana, igual que ella, no sabe, está castrada: el significante de la falta en el Otro.
Al igual que el sujeto-pera, el Otro-manzana está causado por el objeto @.
Si el Otro-manzana goza, el Otro del Otro, el Otro completo, el Otro que sabe, no existe. Esto no es lo mismo que afirmar que el Otro no existe.
No es que no haya Sujeto Supuesto al Saber. Es que el Sujeto de la transferencia está tachado. No se puede pensar el SsS sino es en su losange con el @.
Ya no se trata de un saber sobre el saber, en continuidad con el saber, apuntando al todo saber, sino del saber como medio de goce, de la escisión entre el saber y la verdad.
La cuestión es si hay un discurso que pueda hacer hueco (y eco) a lo real. Esta es la apuesta del discurso del psicoanálisis: que el síntoma pueda trasvasar su real (junto con su angustia) al discurso. Para ello, es necesario no tanto un discurso hueco (como el de algunos psicoanalistas, que suena a lata vacía) como un discurso con huecos. Esto es lo más difícil de sostener en un psicoanálisis.
 |
| El Otro-manzana tachado por el significante |
En la realidad, donde las frutas no hablan, esto es un disparate, un contrasentido. En el campo del lenguaje, en el sistema del significante, donde los términos se sostienen en su oposición recíproca, en su relación de diferencia, es la ley: para saber lo que es una pera hay que preguntárselo a lo que no es una pera, a la manzana, el Otro de la pera. Repetimos que la manzana no tiene la respuesta. También se puede decir que la respuesta es la falta de respuesta; ergo, la falta.
Cuando nos referimos al lugar de la estructura como un lugar de lugares, en correspondencia mutua, no destacamos lo suficiente la función decisiva del cero como significante del lugar, en tanto lugar vacío. En esta función el cero es homólogo al falo como significante del lugar del deseo.
Saussure, en una especie de astucia psicoanalítica, o de viejo zorro lingüístico, con un olfato privilegiado para los significantes, aconseja que si alguien quiere averiguar cuál es el valor de un determinado significante, lo mejor que puede hacer, para no errar, es no poner el foco sobre ese mismo significante, sino sobre los significantes vecinos, los que le rodean, los que están en su contorno, en las inmediaciones.
 |
| El contorno del significante |
Esto es una consecuencia de que en el lenguaje es más importante el sistema que el término aislado. De hecho, el término individual es en función del sistema, del conjunto.
 |
| El sistema del significante |
Analizando los términos que rodean, que circundan, a un determinado significante, podremos saber cuál es su valor. Porque su valor depende de su relación de oposición, de diferencia, con el valor de los significantes que son vecinos suyos, con los que forma una red, una constelación, la trama de un tejido.
 |
| La constelación del significante |
Tan es así, que si cambia un vecino, o desaparece, inmediatamente cambia el valor del término que se está analizando, sin que él haya cambiado, sin que nada haya cambiado en él. Lo único que ha cambiado es el haz de relaciones, la conformación del campo de fuerzas-valores.
Igual que el valor es otorgado por el Otro, el cambio de valor no depende de ningún cambio en uno, sino de una modificación, alteración, en el lugar del Otro (siempre concebido como un campo complejo de interrelaciones, de anudamiento entre elementos disìmiles).
Esta versión es una especie de interpretación laica o científica, desde la lingüística, del Dime con quien andas y te diré quién eres. O del ortegüiano: Yo soy yo y mi circunstancia, a condición de tachar el Yo soy yo, ya que aquí lo que domina, lo que constituye la ley, es el Yo soy Otro de Rimbaud. El Yo es lo que el Otro dice de él.
De esta forma, se constituye un campo ético, regido por la presencia enigmática del prójimo, no por el altruismo y otrismo del semejante.
La posición de Saussure es radical con respecto a este Yo no soy yo sino mis vecinos, y su corolario necesario: Yo soy Otro. Para Saussure, en el sistema de la lengua, en su relación de sincronía, de simultaneidad, sólo hay diferencias. No hay primero un conjunto de términos y luego la diferencia entre ellos. En el sistema no hay entidades positivas, sólo hay diferencias entre valores. Un significante es una pura negatividad,: es lo que no es, lo que los otros no son.
Esto es algo que choca contra el sentido común, que linda con la paradoja, convirtiendo al sistema de la lengua, por causa de su negatividad, en algo difícil de concebir desde lo imaginario. Entonces, Saussure, se tiene que apoyar en determinados ejemplos para transmitir esta negatividad de la lengua en la que sólo hay diferencias significantes sin una positividad a la que la representación se pueda agarrar para no despeñarse.
El lenguaje comporta un efecto necesario de castración, debido a la separación, la spaltüng, entre el orden del significante y el flujo del significado.
 |
| El valor del sistema de la lengua |
El lenguaje comporta un efecto necesario de castración, debido a la separación, la spaltüng, entre el orden del significante y el flujo del significado.
Saussure toma el ejemplo del trayecto de un tren. Cualquier tren que se encuentre en la guía de los ferrocarriles puede servir. Tomemos el caso del tren de Madrid a Toledo de las 16, 45 H.
 |
| La identidad significante del tren |
Hay que procurar elucubrar lo menos posible porque si no podemos extraviar nuestro destino y no llegar a buena estación. Si se piensa hay que pensar en términos significantes (pensar con los significantes).
Contamos con cuatro significantes: tren; Madrid; Toledo; 16, 45 H. Mientras más vacíos de sentido estén, mejor que mejor. Porque lo que nos interesa no es su significado sino sus relaciones recíprocas, su valor. Leemos: El tren de Madrid a Toledo de las 16,45 H.
¿Qué es lo que le otorga su identidad singular a este tren dentro del conjunto de los trayectos del ferrocarril? Su diferencia con respecto a los otros trayectos. El tren Madrid-Toledo; 16,45H. es lo que los otros no son.
 |
| Los trayectos del significante |
El tren Madrid-Toledo; 16, 45 H. (el guión, el punto y coma, la coma y el punto, también son importantes) es lo que los otros no son: el tren Madrid-Toledo; 23 H., el tren Palencia-Santander; 10H... La particularidad de este tren se sostiene en su relación opositiva y diferencial con el resto de los significantes del conjunto de los ferrocarriles. Y como el otro significante, con el que este significante (al que podemos denominar uno) se sostiene en una relación recíproca, es también lo que los otros no son, todo se reduce, en última instancia, a una relación entre puras negatividades (carentes de cualquier sustancialidad).
El significante tren Madrid-Toledo; 16, 45 H. se puede representar por un blanco en el mapa de los ferrocarriles; mapa que se constituye como una constelación de puntos (representantes de la representación de las estaciones) de los que parten un haz de flechas en todas las direcciones (representantes de los trayectos).
 |
| El significante es un blanco en el mapa |
Aunque desapareciese esa línea férrea, de la que ya solo quedarían unas vías muertas y unas cuantas estaciones fantasmas, el tren Madrid-Toledo; 16,45 H. seguiría existiendo en su condición de significante. Porque la condición de significante no depende de un hecho individual, sino de una función estructural, sistémica; es un valor del conjunto (valor de valores), determinado por la coexistencia, la simultaneidad, entre términos (desprovistos de cualquier sustancia) que se sostienen en una relación recíproca.
 |
| La estación fantasma |
 |
| La vía muerta |
Un significante seguirá estando presente, aún en su ausencia, si persiste el contexto ferroviario, el mapa de ferrocarriles, la guía de trenes.
Por su relación de co-pertenencia a un sistema, co-rrespondiente, co-rrelacionante, valorizante, in-sustancializante, el significante estará presente en su ausencia y ausente en su presencia.
La paradoja mayor es que sin cambiar nada del tren Madrid-Toledo; 16, 45 H., permaneciendo inalterable su trayecto, no dejará de alterarse si se producen cambios en la red de ferrocarriles. La modificación en uno o varios puntos de la red, al tratarse de un tejido conjuntivo, afecta al conjunto.
Si por causa de un bombardeo desapareciese la calle de Serrano (no nos importa ahora que este nombre corresponda a un general), habiéndose conservado el "en-torno" -las calles adyacentes, confluentes, circundantes, perimetrales y perpendiculares-, no haría falta consultar el callejero para ubicar la arteria Serrano en el mapa significante, en el árbol circulatorio de las calles de Madrid, al hacerse presente en su ausencia. como un agujero en la manzana (de Eva, de sidra, sana o podrida, burguesa o proletaria, de calles...).
 |
| La calle de Serrano |
Lo que introduce de original el psicoanálisis es que ese agujero de (en) la manzana es horadado por el gusano del goce (excesivamente voraz).
Lo que se impone aquí son diferencias significantes. La materialidad o consistencia de los trenes no constituye un factor diferenciador. Lo decisivo es la pura diferencia (más allá de todo significado) entre el significante tren Madrid-Toledo; 16, 30 H. y el significante tren Madrid-Toledo de las 23 H. No se trata de la diferencia entre dos trenes sino de lo que anuda, en su oposición, a un par significante (S1-S2).
Esa oposición no opone otra cosa que diferencias significantes, valores sincrónicos (en realidad, nadas).
Significante es igual a diferencia debido a que solo emerge en su identidad en la relación con los otros significantes, los que no-son-él; igual que él es lo que no-son-los-otros.
Nadie es lo-que-es sino lo-que-no-es. Los significantes son heracliteanos, no parmenideanos.
El sistema de la lengua es un haz de líneas y puntos por el que circulan y se transmiten negatividades, en su atracción y repulsión por los nudos del goce (es un sistema kandiskyano).
Significante es igual a diferencia debido a que solo emerge en su identidad en la relación con los otros significantes, los que no-son-él; igual que él es lo que no-son-los-otros.
Nadie es lo-que-es sino lo-que-no-es. Los significantes son heracliteanos, no parmenideanos.
 |
| El significante prende el mundo, lo inflama de goce |
El sistema de la lengua es un haz de líneas y puntos por el que circulan y se transmiten negatividades, en su atracción y repulsión por los nudos del goce (es un sistema kandiskyano).
 |
| El sistema kandinskyano del significante |
II) La unidad fragmentada del lenguaje
Saussure se plantea la pregunta por lo que constituye la unidad del lenguaje. Su conclusión es que no es ni el significante ni el significado, sino la relación entre los dos que se articula como signo lingüístico.
Otra vez nos encontramos con la relación, que anuda diferencias, negatividades, nadas.
No son realidades sino relacionadidades: nudos vinculares que se vinculan a través de tramas vinculares con otros nudos vinculares que se vinculan...hasta el infinito.
Tejidos vecinales que se avecinan en vecindades de vecinos avecinados avecinantemente avecinantes.
 |
| El tejido vecinal |
El sujeto es el que hace la historia en tanto versión singular, relato, cantar de gesta, epopeya, sobre los nexos de nexos de nexos.
Nexos de nexos anexados a nexos conexos a anexos anexantes de nexos de nexos...
 |
| El trabalenguas |
No todo son nexos. También hay falta de nexos o nexos faltantes, Y, ¡cómo no!, nexos a causa de falta de nexos.
No todo es insustancial, insignificante. Entre tantos nexos están los anexos conexos a la sustancia del goce. Los hilos sutiles y tenues de los pensamientos se diluyen bajo el peso del nudo en la garganta, la punzada en el pecho, el corazón en un puño, el puñetazo en la boca del estómago, el dolor en el vientre, la respiración agitada, los presentimientos sombríos, las sombras ominosas, los recovecos nunca explorados del alma agitada.
 |
| La sombra del cuerpo |
Lo que importa no es el significante o el significado en sí mismos (si es posible concebir un en-sí-mismo en el lenguaje, que está más bien hecho de un en-el-Otro), sino la articulación, en su diferencia, entre el significante y el significado.
Lo que vincula a los dos elementos del signo lingüístico es su oposición. De ahí, la presencia de la barra, que, al mismo tiempo, anuda y separa.
Saussure es categórico, el significante y el significado, como una pareja bien avenida, no pueden vivir separados.
El significante sin su querido significado es una pura materia sonora, sin separación entre sus emisiones, que no se constituirá como unidad, delimitada y sucesiva.
El significado sin su amado significante es impensable, al transformarse en un magma, en una masa amorfa, hecho de pensamientos sin ideas.
El significante sin su querido significado es una pura materia sonora, sin separación entre sus emisiones, que no se constituirá como unidad, delimitada y sucesiva.
El significado sin su amado significante es impensable, al transformarse en un magma, en una masa amorfa, hecho de pensamientos sin ideas.
El espíritu vivifica la materia. Y la materia da forma al espíritu.
¿Cómo interviene en la identidad significante del tren Madrid-Toledo; 16, 45 H. su consistencia de tren, su materialidad en tanto objeto real? Saussure es rotundo, no interviene para nada. La prueba es que podemos cambiar el tren de arriba a abajo, o que incluso en ese momento no haya ningún tren en la vía, y, a pesar de ello, el tren Madrid-Toledo; 16,45 H. seguirá siendo el tren Madrid-Toledo; 16, 45 H.
La pérdida de su identidad real no implica la de su identidad significante, que se sostiene en la sincronía del sistema de los significantes: un significante es lo que los otros no son; un tren es lo que los otros no son. Lo simbólico se reafirma sobre lo real.
La pérdida de su identidad real no implica la de su identidad significante, que se sostiene en la sincronía del sistema de los significantes: un significante es lo que los otros no son; un tren es lo que los otros no son. Lo simbólico se reafirma sobre lo real.
Si a ese tren que nos interroga por su estatuto lo pintamos de verde o de añil seguirá siendo el mismo tren: el tren Madrid-Toledo; 16, 30 H., con punto y coma. Esto demuestra que el significante no se sostiene en una referencia cualquiera al referente. Ya podemos vestir a la mona de seda que mona se queda. Ya podemos pintar a la mona del significante de amarillo que significante se queda.
 |
| El significante vestido de seda |
El significante se sostiene en su relación opositiva con el conjunto de los significantes, produciendo un efecto de significación (metafórico o metonímico).
Eso no quiere decir que el referente no exista. Existe el tren, con su vagón amarillo, pero es conveniente estar muy atentos al significante, a sus horarios y honorarios, para no perder el tren. Si nos quedamos muy fascinados por sus vivos colores y olvidamos que el tren habla, a lo mejor no llegamos a tiempo.
 |
| El tren-significante viaja por las vías de lo real |
Entonces, ¿qué importancia tiene el referente, el tren de carne y hueso, que podemos ver con nuestros ojos y tocar con nuestras manos, que nos lleva graciosamente a nuestro destino en Toledo? Desde el punto de vista de su identidad como significante, lo que hace de ese tren ese tren y no otro, ninguna.
La identidad de un significante, aunque sea ferroviario, no se sostiene en su función de representación de un significado.
La identidad de tal tren, tal cual, tal y tal, no encuentra su fundamento en la materialidad del tren tal.
En el sistema de la lengua, por in-consistir en un juego de valores simbólicos, de puras diferencias sin términos positivos, la naturaleza material del objeto, al ser elevada a la condición de rasgo, de marca o trazo de escritura, se disuelve, solo interviene como un elemento negativo (aunque existir existe).
 |
| El significante como trazo de escritura sobre el cuerpo |
Hay que repetirlo, porque todo se basa en la repetición, un significante es lo que los otros no son.
III) Juanito, Jorgito y Jaimito
Tomemos el caso de Juanito, Jorgito y Jaimito, los sobrinos del Pato Donald. ¿Quién es Juanito en su identidad de sujeto del significante?. Él no sabe lo que es. Juanito no es igual a Juanito. Para saber quién es tiene que dirigirse al lugar del Otro.
 |
| La identidad conjunta de Juanito, Jaimito y Jorgito |
Juanito es lo que Jorgito y Jaimito no son. Se puede afirmar que Juanito es lo que les falta a Jorgito y a Jaimito para ser Jorgito y Jaimito.
¿Lo que les falta a Jorgito y a Jaimito es Juanito? No, lo que les falta, lo que por siempre les faltará, y no cejarán de buscar, está más allá de Juanito. Lo que les falta es el deseo.
Juanito, para saber lo que es como Juanito, sin remedio, sin falta, deberá tachar a Jorgito y a Jaimito. Tendrá que marcarles con la barra del significante.
No tendrá más recurso, a falta de otra cosa, que abolir al Otro. Esta es la operación de tachadura que produce un Otro causado por un objeto enigmático. Lacan, a este objeto, lo escribe con la letra @; una letra cualquiera,
Todo el truco consiste en hacer una jaimitada. O una juanitada o jorgitada. La jaimitada, necesaria para saber-se, es la de tacharse o abolirse a sí mismo. Operación de auto-barramiento, de auto-marcación, que me borra, me divide como sujeto, me constituye como un no-sé.
Entonces, me callo. Sabiendo que no puedo decir todo, digo lo que no-sé (la pasión por la ignorancia). Digo lo inconsciente. Soy dicho por los significantes del inconsciente, por el discurso del Otro.
Si Juanito tiene que tachar, que borrar, a Jorgito y a Jaimito para saber quién es... Jorgito y Jaimito, a su vez, también tienen que tachar a Juanito para poder saber quiénes son. Entonces, en este juego, todos están tachados. El sujeto está tachado en su relación con el Otro. El Otro está tachado en su relación con el sujeto. Es un duelo de tachaduras.
Donde están las tachaduras, barraduras, borraduras, aboliciones varias, es la oportunidad, el momento, el resquicio, que el goce ladrón y libertino elige para entrometerse, atravesarse, hacer acto de presencia: ¡Aquí estoy!
La relación es siempre entre un sujeto tachado y un Otro tachado, más allá de la relación entre un moi y un i (@). Sujeto y Otro pueden ser el pueblo de Israel y su Dios.
Entre el sujeto tachado y el Otro tachado hay un entre que tiene la función de operador lógico: el objeto @. Es un operador, un vel lógico, que anuda, en el sentido de que vincula y separa.
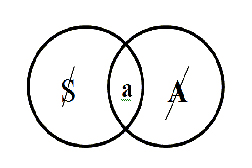 |
| El @ en la intersección vacía entre el sujeto y el Otro tachados |
El @ no es un significante, sino una letra, una escritura. Las letras no son la representación escrita de los fonemas del alfabeto. La letra es una marca, una incisión, en el cuerpo. Por este motivo, tiene el carácter de trazo escrito.
El @ no es un significante. Es un objeto. La letra @ es la marca de un objeto.
El objeto no tiene el valor absolutamente relativo, insustancial, inconsistente, in-significante, del significante. El significante solo ek-siste en su sobredeterminación, en la relación de sincronía, de simultaneidad, de reciprocidad, a nivel del sistema.
La relación del sujeto por su inscripción en el sistema del significante es la de la falta-en-ser.
El objeto, al no ser un significante, es poseedor de una sustancia, la del goce. No es inconsistente sino que tiene una consistencia, la del cuerpo. El Otro es el cuerpo.
La letra @ es la escritura del objeto del deseo y del goce. Es una escritura cuya superficie de inscripción es el cuerpo. El instrumento de escritura es el significante en su incidencia de corte sobre el cuerpo.
IV) Valor absoluto y valores relativos. Valor objetal y valor significante. Valor de deseo y valor de demanda.
El valor del significante es un valor relativo, sistémico. Se sostiene en la pura diferencia, sin términos positivos. Lo podemos representar por un haz de flechas, con un momento negativo.
El valor del objeto es un valor absoluto; es el valor oro del sistema de los significantes. No está sujeto a las subidas y bajadas, a los flujos y reflujos, de los valores cambiantes, relativos, de los significantes (monetarios u otros), en sus correspondencias.
El objeto @ tiene un valor de goce. El significante tiene un valor de cambio. No hay proporción entre ambos valores. Su distancia es inconmensurable, insalvable. Esto nos confronta a la fractura del sujeto, a su spaltüng, a su hiancia irreductible.
El objeto @ detenta la única sustancia que hay en un psicoanálisis: la del goce. En este sentido, tiene un valor absoluto, ya que se constituye como el patrón de medida de todos los valores del significante. Por eso lo comparábamos con el patrón oro del sistema monetario.
 |
| El patrón oro |
Si el patrón oro (el objeto @) tiene un valor sólido, que se puede almacenar, ver y tocar; el significante (el sistema monetario) tiene un valor fluido, de carácter totalmente relativo.
El significante es pura diferencia. El oro del Rhin, el @ del Otro, el cuerpo hablado, es consistencia gozosa.
Lacan trabaja la relación entre el objeto @ y el número de oro, la proporción áurea. El @ es el número que establece la proporción de lo que no tiene proporción. Es la cifra de la media y extrema razón del deseo.
No hay proporción ni proporcionalidad entre el goce macho y hembra. Pero hay un patrón de medida, el número de oro, que establece el valor de goce que rige y ordena todo el intercambio de los significantes, su trabajo, en el contexto del sistema de producción.
La riqueza de la naciones, según Adam Smith, depende de los bienes producidos. Según Carlos Marx, en esta acumulación de bienes, producto del trabajo, se atraviesa un resto, que tiene función de exceso, que actúa como un síntoma en el conjunto del sistema de producción capitalista. De este resto, de la plusvalía, de ese tiempo de trabajo no pagado, se apropia el capitalista en detrimento del obrero, que resulta despojado del beneficio de su propio trabajo.
En el lugar de la plusvalía el psicoanálisis sitúa una pérdida de goce estructural, así como una posibilidad de recuperar ese beneficio sustraído al trabajador, a través del plus de gozar.
V) Necesidad, demanda y deseo.
La necesidad concierne al organismo.
La demanda resulta del atravesamiento de la necesidad por el desfiladero del significante.
La demanda, en tanto demanda de amor, es incondicionada.
Una parte de la necesidad escapa a la captura por la demanda significante. Reaparecerá como condición absoluta en el plano del deseo.
El cuerpo de la demanda es el cuerpo simbólico.
Los significantes de la demanda -orales, anales, etc.-, giran alrededor del borde erógeno del agujero pulsional (la boca, el ano, el borde palpebral, etc.).
 |
| Los objetos de la demanda y del deseo |
El objeto @ ocupa el centro del orificio pulsional, del agujero simbólico, efecto del corte significante sobre el cuerpo.
VI) La identidad significante y la materialidad del tren
Insistimos, podemos viajar en el tren-significante Madrid-Toledo; 16, 45 H. gracias al otro tren-significante Madrid-Toledo; 23, 00 H., en el que no vamos a viajar, pero sin el cual nunca sabríamos en qué tren estamos viajando.
Solo hay una forma de resolver todas estas diferencias: a pares. O jugando a pares y a nones (a un juego de azar).
La referencia a la naturaleza material del tren aquí no cuenta para nada. No es un valor. Lo que sí que interviene es la materialidad del significante que no es un ente espiritual, un alma sin cuerpo, que flota en el éter. El significante habita en y entre los cuerpos, alterándolos.
No sólo esto, a través del significante se establece el lazo social con los otros. La materialidad del significante es la del nudo, el lazo, la trenza. También, la del encuentro.
Saussure plantea que lo que constituye la unidad del sistema de la lengua no es la materia sonora, el sonido aislado, sino la diferencia entre los sonidos, entre la imágenes acústicas. El corazón de la maquinaria del significante, el centro motor, es la diferencia.
Uno puede atacar esta posición rígidamente estructuralista de Saussure utilizando un argumento realista con el que se argumenta desde las evidencias incontestables de la realidad. El problema es precisamente ese, el carácter in-contestable de la realidad, que no admite respuestas, argumentos, que no es dialéctico.
El argumento, de un orden absolutamente práctico, en el que lo que es es, podría ser este: Si no hay tren no se podrá ir de Madrid a Toledo. Nada que discutir. No hay más que decir. Lo has dicho todo.
Nadie niega la existencia del tren y sus prestaciones como vehículo. Pero lo que estamos discutiendo es el estatuto del tren como significante, incluido en el sistema de las comunicaciones ferroviarias (y en el sistema, más general, de los medios de transporte).
Estamos en la ditmensión de las líneas férreas por las que, es cierto, circulan los trenes, pero cuyo trazado se ha dibujado y calculado previamente en un plano (con lápiz y papel).
El argumento, de un orden absolutamente práctico, en el que lo que es es, podría ser este: Si no hay tren no se podrá ir de Madrid a Toledo. Nada que discutir. No hay más que decir. Lo has dicho todo.
Nadie niega la existencia del tren y sus prestaciones como vehículo. Pero lo que estamos discutiendo es el estatuto del tren como significante, incluido en el sistema de las comunicaciones ferroviarias (y en el sistema, más general, de los medios de transporte).
 |
| La materialidad significante del tren |
Estamos en la ditmensión de las líneas férreas por las que, es cierto, circulan los trenes, pero cuyo trazado se ha dibujado y calculado previamente en un plano (con lápiz y papel).
Para ir de Madrid a Toledo es evidente que hay que utilizar un tren. Pero sólo con un tren no se va a ninguna parte.
Para escribir una demostración de lógica matemática en la pizarra se necesita tener una tiza. Pero una tiza sola no posibilita a nadie escribir los enunciado lógicos con los que se prueba un teorema de las matemáticas.
Está esa expresión de un tonto con una tiza. Aunque la inteligencia no es una herramienta imprescindible para desplegar una demostración de lógica formal, es necesario, para ello, saber de álgebra simbólica. El saber en juego no es del orden del conocimiento, sino pragmático, en el sentido de un saber hacer, en una praxis, con las letras, con los significantes.
Para hacer que circule un tren de Madrid a Toledo hay que aplicar diferentes saberes: física, resistencia de materiales, dinámica de motores, topografía, etc. En síntesis, hay que ser ingeniero y físico-matemático (lo que puede parecer sorprendente).
 |
| El orden del significante se sostiene en las leyes del discurso |
Para que un tren viaje de Madrid a Toledo hay que rellenar y manchar muchas hojas con cifras matemáticas, ecuaciones, letras, variables, etc. Hay que sudar tinta producida por el trabajo de calcular, por la pasión algebraica (que convierte cifras en letras). Se trata de operar con las masas y resistencias de lo real desde la lógica simbólica. Hay que adherirse a la corriente del formalismo-materialismo.
Es evidente que la escritura de lo simbólico tiene un efecto sobre lo real (de significación y de goce). Gracias a esas fórmulas matemáticas que abren surcos en la continuidad de lo real, a través de los cuales circulan las vías del tren, éste se puede desplazar de Madrid a Toledo.
Son las letritas, las variables algebraicas, las ecuaciones matemáticas, toda esa orgía de símbolos, el verdadero motor del tren, el Primer Motor aristotélico, que pone al mundo en movimiento.
Que la causa material resida en esas letritas menstruales, que miden (de mensis) lo real, es algo sangrante para el narcisismo, un verdadero insulto a la inteligencia.
En última instancia, lo que es eficaz sobre lo real, mortificante-vivificante, es la instancia de la letra en el discurso del inconsciente.
 |
| La lógica del significante y su valor de verdad |
VII) El signo cero y el goce
¿Qué del goce? ¿Hay goce o ha desaparecido el goce a causa de la mortificación producida por el significante? ¿Qué del cuerpo?
Es obvio que hay goce. Lo que sucede es que el goce no es un observable. El goce se inscribe en el campo de las Ciencias Conjeturales, que es el del discurso
El goce se puede escribir. Todas las lápidas escriben uno... ¡o ninguno! Esas letritas del álgebra no es que expresen el goce, que es inexpresable, sino que producen goce.
El goce se puede escribir. Todas las lápidas escriben uno... ¡o ninguno! Esas letritas del álgebra no es que expresen el goce, que es inexpresable, sino que producen goce.
 |
| El goce se siente y se escribe |
Vamos a ir al ejemplo del ajedrez para abordar esta cuestión del significante y el goce.
Aparentemente, el goce con el que trabajamos en la experiencia psicoanalítica (esa materia altamente explosiva a la que se refiere Freud) no tiene nada que ver con el del juego del ajedrez (que haberlo hailo).
Saussure toma el juego del ajedrez como un paradigma para dar cuenta de la estructura y las leyes que rigen el sistema de la lengua, al encontrar entre ellos una fuerte homología.
Antes que nada, como una tarea preliminar, voy a volver al cero.
Es evidente que el cero es un número, aunque no lo parezca, porque el cero no cuenta nada, o cuenta nada (¡o cuenta cero!).
El cero es un símbolo. Eso también es algo evidente. Es tan simbólico o tan poco simbólico como el Uno. De hecho forman la pareja fundamental del sistema de los números.
El cero es el símbolo de un lugar vacío -por ejemplo, en la numeración posicional-. El lugar vacío, en la secuencia numérica ordenada, no está ocupado por ningún otro número diferente al cero. Ese lugar vacío, en el que falta el número, hay que poder leerlo, contarlo, para que, por ejemplo, se pueda diferenciar entre el 4 y el 40.
El cero es el significante del lugar vacío. De esta guisa, es el significante del deseo.
 |
| 0 + 1 = 0 |
El cero es un símbolo. Eso también es algo evidente. Es tan simbólico o tan poco simbólico como el Uno. De hecho forman la pareja fundamental del sistema de los números.
El cero es el símbolo de un lugar vacío -por ejemplo, en la numeración posicional-. El lugar vacío, en la secuencia numérica ordenada, no está ocupado por ningún otro número diferente al cero. Ese lugar vacío, en el que falta el número, hay que poder leerlo, contarlo, para que, por ejemplo, se pueda diferenciar entre el 4 y el 40.
El cero es el significante del lugar vacío. De esta guisa, es el significante del deseo.
El cero es el número de la discordia, que se atraviesa entre un número y otro como algo molesto, perturbador; incluso puede ser un número inquietante, hasta angustiante, con el que es difícil llegar a acuerdos. Esto no es psicología de los números o numerología.
El Uno es el número de la concordia. Todos nos queremos reunir, juntar, alrededor del Uno; hacernos Uno. Pero, desgraciadamente, siempre nos topamos con la imposibilidad, con la castración, que nos obliga (por mor de la falta) a poner un número más. A este número-en-más le llamamos el sucesor. Que exista la función del sucesor es el índice de la incompletitud que afecta al conjunto de los números naturales.
El cero se inventó en la India. Fueron los árabes los que lo introdujeron en Europa. El término árabe para cero es sifra, que significa vacía. Este término da lugar a cifra.
Por consiguiente, vacía, remite tanto a cero como a cifra. Es llamativo que el cero, la sifra, sea el vacío en el género femenino: vacía. ¿Por qué?
Por consiguiente, vacía, remite tanto a cero como a cifra. Es llamativo que el cero, la sifra, sea el vacío en el género femenino: vacía. ¿Por qué?
Probablemente esto haga referencia al goce femenino, al vacío de la mujer, a la mujer que se hace vacía. Es verosímil que exista una relación privilegiada entre la mujer y el cero, entre la mujer y el vacío, vía el goce femenino, no-todo fálico.
Aunque se pueda pensar que es un ejercicio de ciencia-ficción, no habría que descartar que la inventora del cero pudiera haber sido una mujer; o que el cero se haya inventado en el seno de una comunidad de mujeres. De hecho, aunque este detalle es banal, el cero tiene formas redondeadas, femeninas, como las curvas del cuerpo de una mujer (una tendencia a lo cóncavo). En cambio, el Uno es un rasgo estilizado, recto, erecto, de carácter fálico, predominantemente masculino (tendiente a lo convexo, sino a lo obtuso).
El signo cero, en los Mayas, se representa con una figura que parece un pan cocido o una labor de costura (una especie de almohadón). Un objeto de fabricación femenina.
VIII) La partida del análisis
Saussure toma como modelo el ajedrez para dar cuenta de la estructura de la lengua en su sincronía, porque lo importante en el ajedrez es el sistema, la correspondencia de las piezas en su relación de simultaneidad, en su estatismo, no en su secuencia.
En el ajedrez existe una dominancia de la sincronía sobre la diacronía.
Saussure toma como modelo el ajedrez para dar cuenta de la estructura de la lengua en su sincronía, porque lo importante en el ajedrez es el sistema, la correspondencia de las piezas en su relación de simultaneidad, en su estatismo, no en su secuencia.
En el ajedrez existe una dominancia de la sincronía sobre la diacronía.
El ajedrez, como todo juego, se basa en leyes, en reglas. Cada una de las piezas, en su movimiento singular, es la cristalización de una regla.
Al ser un juego de estrategia lo importante es el sistema, el estado actual de la partida.
Referirse a sistema es hablar de orden sincrónico, de relaciones de simultaneidad, de la posición recíproca de las piezas en el tablero, de su interacción.
Es tal la importancia del sistema, del despliegue de las piezas en el campo de batalla, que, dice Saussure, si alguien llegase en mitad de una partida, sólo se interesaría por el estado actual de la partida, por la dis-posición de los dos ejércitos en el tablero de batalla, y obviará la secuencia de movimientos que han llevado a ese estado (la historia de la partida).
Lo importante es el estado, el orden estático, fuente de un profundo dinamismo, en donde se pueden leer todos los cambios potenciales.
En una estructura formal y temporal residen todas las infinitas potencialidades de la partida: los movimientos.
¿Qué es lo que sucede si se extravía uno de los caballos y no hay ningún otro de repuesto? No pasa nada. Solo se trata de una figura, de la figuración de una regla, que puede ser sustituida por cualquier otra. Incluso por una figura des-figurada, des-cabalgada, cuya apariencia imaginaria no tenga nada que ver con la del caballo. Por ejemplo, por una simple y vulgar piedrecita zigzagueante.
El movimiento del caballo no es el movimiento de ningún caballo. Es un movimiento en zigzag, quebrado, que se puede proyectar en sus líneas sobre la superficie del tablero.
Si se conoce la regla de juego que rige el movimiento del caballo, su identidad significante, su valor propio, en su diferencia con el valor del resto de las piezas, uno podrá sustituir el caballo perdido por cualquier cosa, y continuar la partida como si nada. Se ha preservado no la figura imaginaria del caballo, sino el significante-caballo, perteneciente al conjunto de la caballería significante.
Al ser un juego de estrategia lo importante es el sistema, el estado actual de la partida.
Referirse a sistema es hablar de orden sincrónico, de relaciones de simultaneidad, de la posición recíproca de las piezas en el tablero, de su interacción.
Es tal la importancia del sistema, del despliegue de las piezas en el campo de batalla, que, dice Saussure, si alguien llegase en mitad de una partida, sólo se interesaría por el estado actual de la partida, por la dis-posición de los dos ejércitos en el tablero de batalla, y obviará la secuencia de movimientos que han llevado a ese estado (la historia de la partida).
Lo importante es el estado, el orden estático, fuente de un profundo dinamismo, en donde se pueden leer todos los cambios potenciales.
En una estructura formal y temporal residen todas las infinitas potencialidades de la partida: los movimientos.
¿Qué es lo que sucede si se extravía uno de los caballos y no hay ningún otro de repuesto? No pasa nada. Solo se trata de una figura, de la figuración de una regla, que puede ser sustituida por cualquier otra. Incluso por una figura des-figurada, des-cabalgada, cuya apariencia imaginaria no tenga nada que ver con la del caballo. Por ejemplo, por una simple y vulgar piedrecita zigzagueante.
El movimiento del caballo no es el movimiento de ningún caballo. Es un movimiento en zigzag, quebrado, que se puede proyectar en sus líneas sobre la superficie del tablero.
Si se conoce la regla de juego que rige el movimiento del caballo, su identidad significante, su valor propio, en su diferencia con el valor del resto de las piezas, uno podrá sustituir el caballo perdido por cualquier cosa, y continuar la partida como si nada. Se ha preservado no la figura imaginaria del caballo, sino el significante-caballo, perteneciente al conjunto de la caballería significante.
 |
| Las figuras son significantes |
Pasa lo mismo con el tren como vehículo, en su materialidad, que puede ser sustituido por cualquier otro. Lo importante es la identidad significante del tren, las coordenadas significantes que lo diferencian de los otros trenes dentro del sistema ferroviario; su insistencia significante -la hora de salida y de llegada entre dos puntos significantes- más que su consistencia imaginaria (su figura); el tren como soporte de un texto y de una textura significante.
¿Y qué del goce? ¿Hay goce en el ajedrez? ¿Hay goce en la lógica simbólica? ¿Hay goce en el sistema de la lengua? ¿Quién goza? Goza el Otro. Esto es lo que hace tan difícil la captación del goce.
En la la lógica simbólica, matemática, hay goce precisamente por la incompletitud e inconsistencia de sus sistemas y aparatos de escritura (por lo menos, falta una letra, la del goce: la R de la relación sexual, que no hay). Esto fue demostrado con los dos teoremas de K. Göedel.
El sistema de la lógica, en tanto estructura simbólica, está agujereado; esto permite la fuga y producción de goce.
La historia de los grandes científicos, sus tragedias, locuras y extravíos, confirma sin duda la existencia del demonio del goce, que habita en los agujeros de las matemáticas, en los intersticios de su lenguaje lógico, que no es el lenguaje del lenguaje, es decir, el metalenguaje que evita los malentendidos del lenguaje.
En el caso del ingeniero que pone en marcha el tren, y, para ello, tiene que garrapatear muchas cuartillas, llenas de símbolos, cuentas y ecuaciones, también hay goce. Lo que pasa es que éste no está a la vista, no es evidente, mucho menos objetivable.
Si miramos en la papelera del ingeniero nos la encontraremos llena de papeles, llenos de símbolos, hechos un burruño, desechados por inservibles. Son las letras (letter) caídas, arrojadas, rechazadas a la basura (litter). Son la letra o litter del goce, los restos, que no han podido ser metabolizados, digeridos, asimilados, por la maquinaria del significante, por el discurso del amo en su forma más eminente: el discurso de la ciencia.
 |
| La letter-litter del goce |
Además, está la sudoración del ingeniero. Esas gotas de sudor que se evaporan de su cuerpo, que se pierden como energía útil, eficaz: la entropía.
 |
| Las gotitas de sudor del ingeniero |
El ingeniero, aunque no pertenezca a la clase proletaria, no dejará de estar explotado por el discurso del amo, produciendo plusvalía, ese excedente de goce, que, indefectiblemente, le será arrebatado. Al estar capturado en las relaciones de producción deberá confrontarse al abismo de su plus-de-gozar.
 |
| El discurso del analista |
Es con este residuo, con lo real de estas letras gozosas, desprendidas del cuerpo de lo simbólico, con las que trabaja el discurso del psicoanálisis. Ese resto, caído en la litter, es el objeto @, causa material del deseo, que, en el discurso analítico, ocupa el lugar de agente, de amo.
El psicoanalista, en la transferencia, hace de semblante de @. Como consecuencia, y esto es decisivo, ocupa una posición de objeto, de resto (de lo-que-resta), no de sujeto.
Su posición remite al goce y no al saber; a la ek-sistencia (real) anudada borromeanamente con la consistencia (imaginaria) y la insistencia (simbólica).
 |
| Georges de La Tour |
¿Y del ajedrez? La pasión del juego nos señala que el goce no está ahí ausente. No es sólo la pasión de ganar; sobre todo, es la pasión a la que arrastran al jugador los significantes del juego, en sus movimientos contingentes, regidos por la leyes del juego, por la táctica y la estrategia.
En el juego del ajedrez, como en todos los juegos en que se juega contra el Otro, en los que se apuesta en relación a su existencia o inexistencia, a su consistencia o inconsistencia, se moviliza un intenso goce.
¿Hay goce en el ajedrez? Hay goce porque se sabe que, excepto en las aperturas y en los finales de partida, el número de jugadas posibles es infinito. En consecuencia, interviene lo incalculable, lo impredecible. Siempre hay un margen para la invención, la creación, el arte (una bella jugada).
No hay más remedio que apostar, que pasar al acto, porque no se pueden controlar, dominar, todos los movimientos significantes del juego.
 |
| Hay que pasar al acto |
En la partida del siglo entre Karpov y Kasparov la pelea era sobre todo política, lo que implica al goce en su más eminente expresión. Era la lucha entre la libertad y el autoritarismo, la nomenclatura burocrática y la invención, la propaganda y la creatividad, el individuo y el estado omnímodo y dictatorial... (por lo menos así lo percibieron muchos en su apasionado compromiso de goce).
En el lenguaje, no se trata de priorizar el sistema de la lengua -sincrónico-, sobre la diacronía. Lo que anuda diacronía y sincronía es el acto del hablante. Es para un hablante que, como tal, manifiesta su pertenencia al cuerpo social, que todo esto, el asunto del goce, le concierne radicalmente en su condición de sujeto.
En la lengua hay goce, hay tiempo, porque interviene, como un hecho decisivo, el acto del sujeto de la palabra ante a un real que le convoca a la hora de la verdad, en la cita con su destino, en el tiempo de la angustia.













































































